A complete list of available videos is available. Links to slides and recordings are included in the abstracts below.
A graphical design is a subset of graph vertices such that the weighted averages of certain graph eigenvectors over the design agree with their global averages. We use Gale duality to show that positively weighted graphical designs in regular graphs are in bijection with the faces of a generalized eigenpolytope of the graph. This connection can be used to organize, compute and optimize designs. We illustrate the power of this tool on three families of Cayley graphs — cocktail party graphs, cycles, and graphs of hypercubes — by computing or bounding the smallest designs that average all but the last eigenspace in frequency order.
You are handed a graph with vertices in a neutral color and asked to color a subset of vertices with \(d\) colors of (increasingly) expensive paints in such a way that only the trivial symmetry preserves the color classes. Your goal is to minimize the number of vertices needing this expensive paint. This paper address the issues surrounding your choices.
A graph is said to be \(d\)-distinguishable if there exists a vertex coloring with \(d\) colors so that only the trivial automorphism preserves the color classes. The smallest \(d\) for which \(G\) is \(d\)-distinguishable is called the distinguishing number of \(G\), and is denoted \(\text{dist}(G)\). A determining set for a graph \(G\) is a subset of vertices whose pointwise stabilizer is trivial. The determining number of \(G\) is the size of a smallest determining set, and is denoted \(\text{det}(G)\).
The cost of 2-distinguishing measures both `how close’ \(G\) is to being 1-distinguishable (in terms of the minimum number of vertices of a final color) as well as the fewest number of vertices that need (re)coloring to achieve a \(2\)-distinguishing coloring. To generalize the concept of cost to \(d\)-distinguishing colorings for \(d>2\), we must separate these two measurement goals.
We can ask how close \(G\) is to being \((d{-}1)\)-distinguishable. This is the minimum size of a color class over all \(d\)-distinguishing colorings. Alikhani and Soltani call this the cost number, and denote it \(\rho_d(G)\). Alternately, we can ask how many vertices we need to (re)color to achieve a \(d\)-distinguishing coloring. This is the minimum size of the complement of a color class over all \(d\)-distinguishing colorings. This is called the paint cost, and is denoted \(\rho^d(G)\).
In this talk, we explore these new symmetries on a variety of graphs.
Topological orientability was first defined by Listing in 1861 followed closely by Möbius (1865); Möbius defined orientation in a compact surface by the existence of a coherent orientation of the edges of a net (polygonal) decomposition of the surface. Only after Euler’s classification of compact surfaces, it was possible to prove that the Möbious combinatorial definition was dependent of the surface and not of the particular polygonal decomposition. This makes orientability both a topological and a combinatorial property. A surface can be orientable or not, and so a given surface can support an orientable or a non-orientable map, but not both. In contrast, bi-oriented and non bi-oriented maps (introduced by Steve Wilson in the seventies under the name of pseudo-orientable maps) can be both present in the same surface.
Despite being only a combinatorial property, bi-orientability has remarkable resemblances with orientability when both are applied to combinatorial objects such as maps.
The present talk, which is an update of the talk given in 2014 JOINT MATHEMATICS MEETINGS, Baltimore, pretends to emphasise the similarities and the differences between them.
Hurwitz groups are the non-trivial finite quotients of the (2,3,7)-triangle group \(\langle\, A, Z \mid A^2 = Z^3 = (AZ)^7 = 1 \,\rangle\), with the name `Hurwitz’ coming from the fact that they are the conformal automorphism groups of compact Riemann surfaces of largest possible order \(84(g-1) = -42\chi\) for given genus \(g \geq 2\) (or given Euler characteristic \(\chi – 2-2g\)). As such, they are also the orientation-preserving automorphism groups of orientably-regular maps of largest possible order \(84(g-1)\) for given genus \(g\) of the underling hyperbolic surface, namely the `Hurwitz maps’, of type \(\{3,7\}\) or \(\{7,3\}\).
Pseudo-Hurwitz groups are the finite smooth quotients of the pseudo triangle group \(\langle\, A, Z \mid A^2 = Z^3 = [A,Z]^4 = 1 \,\rangle\), and as such, are the automorphism groups of regular bi-oriented maps of largest possible order \(48(g-1) = -24\chi\) for given \(\chi = 2-2g \le -2\).
We show that the alternating group \(A_n\) and the symmetric group \(S_n\) are pseudo-Hurwitz groups for all but a small number positive integers \(n\), and in particular, for all \(n > 23\).
A graph \(G\) is $d$-distinguishable if there is a vertex labeling with \(d\) labels so that only the trivial automorphism preserves the labels. The smallest such \(d\) is the distinguishing number, Dist\((G)\). A set of vertices \(S\) is a determining set for \(G\) if every automorphism of \(G\) is uniquely determined by its action on \(S\). The size of the smallest determining set for \(G\) is its determining number, Det\((G)\). The orthogonality graph \(\Omega_{2k}\) is a highly symmetric graph, with vertices that are bitstrings of length \(2k\) and two vertices being adjacent if they differ in precisely \(k\) bits. We show that Det\((\Omega_{2k}) = 2^{2k-1}\) and that if \({m\choose 2} \geq 2k\), then \(2 <\) Dist\((\Omega_{2k}) \leq m\).
In this talk I will describe the complete determination of which of the alternating groups \(A_n\) and the symmetric groups \(S_n\) occur as the automorphism group of some regular or chiral map on an orientable surface, and which of them occur as the automorphism group of a regular map on a non-orientable surface. The situation for some given types \((m,k)\) is also considered, with special focus on types with \(m = 3\), and with \((m,k) = (3,7)\), \((3,8)\), \((4,5)\) or \((4,6)\) and their duals. Some further observations are made about what happens for regular and orientably-regular maps with given valency, and for regular and chiral polyhedra.
Much but certainly not all of what is presented follows from theorems in papers by me and others. This talk brings those and some new observations together.
There is a wealth of data on polytopes and maps, computed and published online in various formats. One of the goals of RAMP (the Research Assistant for Maniplexes and Polytopes) is to make this data easily available in GAP so that researchers can search the data and even enrich it by calculating and storing new properties. There are many interesting challenges, such as: How do we efficiently store the data? How do we make it easy to access and expand?
In this talk I will discuss and demonstrate the library of Small Reflexible Maniplexes in RAMP. Along the way, we will meet many interesting families of maniplexes, and we will discuss how RAMP has helped identify some of these families, and how knowledge of these families helps us to extend our datasets.
RAMP is a joint project with Mark Mixer and Gordon Williams.
I have been completely fascinated by abstract regular polytopes since 2010, two years after finishing my PhD. In this talk I will explain the problems that made me entirely devoted to this topic.
The most prominent example of an abstract regular polytope is the simplex. The automorphism group of the simplex is the simplest Coxeter group, represented by a stretchy line and isomorphic to a symmetric group. The highest rank of an abstract regular polytope whose automorphism group has degree \(n\), is \(n-1\). The simplex, is the only one in the top-level of rank scale. For any symmetric group of degree \(n\) (with \(n\geq 4\)), there exists an abstract regular polytope for every rank \(r\), from \(3\) up to \(n-1\). The remaining transitive groups of degree \(n\), are below midway of the rank scale. The “Aveiro Theorem” states that the maximal rank an abstract regular polytope for the alternating group of degree \(n\) is \(\lfloor n-1/2\rfloor\) (with \(n\geq 12\)). Similarly to the symmetric groups, the rank scale of these alternating groups is an interval.
If we consider the symmetric group of degree \(n\) and we go down in the rank, it seems that the number of abstract regular polytopes is constant (it does not depend on \(n\)). That is true for the ranks \(n-1\), \(n-2\), \(n-3\) and \(n-4\), for which the number of polytopes (up to duality) are \(1,\, 1,\, 7\) and \(9\) respectively. Computational results suggest the sequence \(1,\,1,\,7,\,9, \,11,\,35,\,48,\ldots\), not in the On-Line Encyclopedia of Integer Sequences. How deep can we go with this result? Let us find out when we meet.
Some Open Problems:
- Does the number of highest rank polytopes for the alternating groups depends on the degree \(n\)?
- The set of ranks of alternating groups are intervals (have no gaps), with one exception, which is alternating \(11\). Is there any reasonable reason for that?
- What is the highest rank of a C-group (not necessarily string) representing the alternating group of degree \(n\)? Is it \(\lfloor( n-1)/2\rfloor\)?
- Is \(\lfloor( n-1)/2\rfloor\) the maximal rank of a string group generated by independent involutions (not necessarily a C-group) isomorphic to the alternating group of degree \(n\)?
Let \(G\) be a finite group and \(H,K\) be its subgroups such that \(H\cap K=\{1\}\). The bi-coset graph \(\Gamma_{(G;H,K)}\) is the bipartite graph whose vertices are the left cosets of \(H\) and \(K\) in \(G\), and the adjacency relation is defined via non-empty intersection.
Biregular \((m,n;g)\)-graphs are graphs that consist of vertices of two degrees, \(m\) and \(n\) (with both of the degrees present) and which are of girth \(g\).
Bipartite biregular \((m,n;g)\)-graphs are bipartite \((m,n;g)\)-graphs with the additional property that the two partite sets consist of vertices of the same degree (different for each set). For a given triple \((m,n; g)\) a smallest (with respect to the order) bipartite biregular \((m,n;g)\)-graph is called a \emph{bipartite biregular \((m,n;g)\)-cage.}
In the talk we present a construction of bipartite biregular \((3, 3k; 6)\)-cages which are bi-coset graphs and work when \(k\) is odd and \(6k+1\) is a prime. It turns out that these graphs are closely related to the so-called Netto triple systems.
Finally, a family of small bipartite biregular bi-coset \((3,3k; 6)\)-graphs will be shown such that \(k\) runs through all integers, however the order of the graphs is by the factor 3/2 off in comparison with the theoretical lower bound.
This research was supported by the APVV Research Grants under numbers 17-0428 and 19-0308, and also by VEGA Research Grants 1/0206/20 and 1/0567/22.
This work is joint with Robert Jajcay, Pavol Jánoš, Jozef Širáň, Yan Wang and Martin Mačaj.
Given a maniplex (map or abstract polytope), can we do some operation on it, so that the result has some prescribed symmetry? For example, for non-self dual maps, taking its medial will give us a two-orbit map with 2 orbits of faces. Although we have not been able to solve this question, in an attempt at it, we have defined voltage operations on maniplexes and polytopes. In this talk I will describe such operations and go over some interesting properties about them. This is work with Elías Mochán and Antonio Montero.
The task of finding a \(k\)-regular graph of a smallest order and of a prescribed girth \(g\) is known as the Cage Problem; as smallest \(k\)-regular graphs of girth \(g\) are called \((k,g)\)-cages. The order of a smallest \(k\)-regular graph of girth \(g\) is often denoted by \(n(k,g)\), but the exact value of this order is only known for limited sets of parameters \((k,g)\). As constructions of specific \(k\)-regular graphs of girth \(g\) provide upper bounds on \(n(k,g)\), the main direction of research into the Cage Problem lies in looking for construction techniques that produce \(k\)-regular graphs of girth \(g\) of small orders. A \((k,g)\)-graph of order smaller than any other known \((k,g)\)-graph is called a record \((k,g)\)-graph. Many record graphs have been constructed using the regular voltage lift construction which produces graphs that admit an automorphism group acting semiregularly on the vertex sets of the constructed graphs. The more general permutation voltage graph construction has somehow been overlooked in this context; perhaps due to the much larger space of possible voltage choices. In our talk, we will discuss the potential of the permutation voltage graph construction in the context of the search for cages with special focus on choices that limit the related search spaces.
As is well-known, a vertex-transitive graph is a Cayley graph if and only if it admits a group of automorphisms acting regularly on its set of vertices. It is also generally acknowledged that Cayley graphs constitute an important subclass of the class of vertex-transitive graphs. It is therefore reasonable to assume that generalizing Cayley graphs to \(k\)-uniform hypergraphs, i.e., pairs \((V,{\cal B})\), where \({\cal B}\) consists of \(k\)-subsets of \(V\), \( k \geq 2 \), might lead to interesting insights into the theory of vertex-transitive \(k\)-uniform hypergraphs. Even though several generalizations of Cayley graphs to hypergraphs can be found in the literature, we choose the most straightforward generalization and propose to call a \(k\)-uniform hypergraph Cayley if an only if the hypergraph admits a group of automorphisms acting regularly on the vertex set of the hypergraph. In our talk, we present some basic properties of Cayley hypergraphs, discuss the connection of this concept to some recent results concerning hypergraphs, as well as connections to our project of constructing \(k\)-uniform hypergraphs whose full automorphism group is isomorphic to a prescribed finite group \(G\) and acts regularly on the vertices of the hypergraph.
I will give a survey of some results, both classical and recent, concerning Paley graphs. These will include their discovery by Sachs and independently by Erdös and Rényi, their properties as strongly regular graphs, their connections, due to Paley, Todd and Coxeter, with Hadamard matrices, block designs and compound polytopes, their automorphism groups, their orientably regular surface embeddings, and their infinite analogues.
The Erdös-Ko-Rado theorem, one of the central results in extremal combinatorics, which gives a bound on the size of a family of intersecting \(k\)-subsets of a set and classifies the families satisfying the bound, has been extended in various ways. In this talk I will discuss an extension of this theorem to the ambient of transitive permutation groups and vertex-transitive graphs.
Let \(V\) be a finite set and \(G\) a group acting on \(V\). Two elements \(g,h\in G\) are said to be intersecting if \(g(v) = h(v)\) for some \(v \in V\). More generally, a subset \({\cal F}\) of \(G\) is an intersecting set provided every pair of elements of \({\cal F}\) is intersecting. The intersection density \(\rho(G)\) of a transitive permutation group \(G\) is the maximum value of the quotient \(|{\cal F}|/|G_v|\) where \({\cal F}\) runs over all intersecting sets in \(G\) and \(G_v\) is a stabilizer of \(v\in V\).
The {\em intersection density array} \([\rho_0,\rho_1, …,\rho_{k-1}]\) of a vertex-transitive graph \(X\) is defined as a “collection” of increasing intersection densities of transitive subgroups of \(\text{Aut} X\), that is, for any transitive subgroup \(G\) of \(\text{Aut} X\), we have \(\rho(G) = \rho_i\) for some \(i \in \mathbb Z_k\), with \(\rho_i<\rho_{i+1}\).
In this talk I will present some recent results about intersection densities of certain transitive permutation groups and vertex-transitive graphs of small valencies.
This is a joint work with Ademir Hujdurović, István Kovács, Bojan Kuzma, Dragan Marušič , Štefko Miklavič, Marko Orel and Cyril Pujol.
The \(k\)-rainbow domination function of a graph is a function that assigns a subset of \(\{1,2,\ldots,k\}\) to each vertex of a graph, such that each non-colored vertex has a complete \(k\)-rainbow of neighbours, that is, \(f(v)=\emptyset\) implies \(\cup_{u\sim v} f(u)=\{1,\ldots,k\}\). The \(k\)-rainbow domination number \(\gamma_{rk}(G)\) of a graph is the minimal possible value of weight \(w(f)=\sum |f(v)|\) over all \(k\)-rainbow domination funtions \(f\) on \(G\). Recently, we have shown that the \(k\)-rainbow domination number \(\gamma_{rk}(G)\) of a \(d\)-regular graph for \(d\leq k\leq 2d\) is bounded below by \(\displaystyle{\left\lceil kn/2d\right\rceil}\), where \(n\) is the order of a graph, and determined some necessary conditions for regular graphs to attain this bound. This enabled us to find simpler proofs of some known results on kRD-number for specific graph families and determine exact kRD-numbers for all cubic Cayley graphs over abelian groups, as well as opened several questions on finding \(k\)-rainbow-domination-regular graphs that will be presented in a talk.
In this talk we will further explore voltage operations (introduced in the previous talk by Isabel Hubard). Given a maniplex \(\mathcal{M}\) with symmetry type graph \(\mathcal{X}\) and a voltage operation \(\mathcal{O}\) we can easily calculate the symmetry type graph of \(\mathcal{O(M)}\) with respect to the symmetries of \(\mathcal{M}\) by applying the operation \(\mathcal{O}\) to the graph \(\mathcal{X}\). We will use this construction to study voltage operations applied to regluar (reflexive) maniplexes and to describe the composition of two voltage operations as a voltage operation. We will also characterize all the operations that can be viewed as voltage operations with respect to a constant voltage operator. If time allows it we will also explore when the operated maniple \(\mathcal{O(M)}\) has extra symmetries that do not come from symmetries of \(\mathcal{M}\), but from symmetries of the operation \(\mathcal{O}\).
The concept of regular covering between graphs and maps belongs to the core of topological and algebraic graph theory. There is a close relation to disrete actions of groups on surfaces and (branched) regular coverings beween surfaces. It forms a bridge between discrete and continuos mathematics. We discuss several equivalence relations introduced on coverings and explain their counterparts in the theory of Riemann surfaces. On the graph and map coverings side we explain the equivalences in terms of voltage assignments. Better understanding of the equivalences allows us to simplify comparison of different coverings, and it is necessary to enumerate the coverings or discrete actions. At the end of my talk I will list several open problems and mention on-going projects.
Joint work with M. Skyvová and J. Karabáš.
The group generated by the standard dual operator and the Petrie operator acts on all fully regular maps and is well-known. Meanwhile, given a fully regular map of valency \(k\), the set of valid hole operators acting on this map are known to form a group isomorphic to the group of units modulo \(k\). It is straightforward to compose hole operators with the Petrie operator. However, things get more complicated if you want to involve the dual operator. That is what I will be exploring in this talk. I will present some results which apply in general, and some which are specific to groups of operators acting on the set of fully regular maps with given automorphism group \(SL(2,q)\), where \(q\) is even.
An orientably-regular map is an embedding of a connected graph on a compact orientable surface such that the group all orientation-preserving automorphisms of the embedding is transitive on arcs. In 2010 M. Conder, T. Tucker and the author classified orientably-regular maps on surfaces of genus \(p+1\) for prime \(p\), part of which relied on computational results of M. Conder. In the talk we will outline how this computational assistance can be avoided.
This research has been supported by the APVV Research Grant No. 17/0428.
Let \(S\) be an orientable surface of genus \(g\). Denote by \(Hom^+(S)\) its group of orientation-preserving homeomorphisms. We say that a finite group \(G\) acts on \(S\) if there is monomorphism \(\varepsilon\colon G\to Hom^+(S)\). Every action may be constructed by means of a pair of Fuchsian groups \(K\triangleleft \Gamma<PSL(2,R)\) acting discontinuosly on the upper half plane \(U\) and an epimorphism \(\eta\colon \Gamma\to G\) with kernel \(K\), where \(K\) is a surface group. Such an epimorphism will be called order preserving. The epimorphism \(\eta\) is constructed from \(\varepsilon\) and a homeomorphism \(U/K\cong S\). Two such actions are equivalent if and only if there is an automorphism \(\alpha\in Aut^+(\Gamma)\) and an automorphism \(a\in Aut(G)\) such that the respective order preserving epimorphisms satisfy the relation \(\eta_2=a(\eta_1\alpha)\). In my talk I will discuss the problem of determining of equivalence classes of discrete actions. In particular, we investigate the action of \(Aut^+(\Gamma)\) on the set of epimorphisms \(Epi_o(\Gamma,G)\) for a finite group \(G\) and a Fuchsian group \(\Gamma\). In case of planar Fuchsian groups, that means groups with signature \((0;m_1,\dots,m_r)\), we present a complete answer giving rise to an algorithm constructing the equivalence classes. I present a list of such actions of small genera. In the general case, we have a partial result.
Joint work with Roman Nedela and J. Karabáš
Slides, video.
More than 50 years ago Tutte observed that if a group \(G\) acts vertex- and edge-transitively on a graph \(\Gamma\) of odd valency then \(G\) also acts arc-transitively on \(\Gamma\). This is of course not true for groups acting on graphs of even valency, and as it was soon demonstrated by Bouwer there are in fact examples where the full automorphism group of a graph acts vertex- and edge-transitively, but not arc-transitively. Such graphs are called half-arc-transitive and more generally a group of automorphisms is said to act half-arc-transitively on a graph \(\Gamma\) if it acts vertex- and edge- but not arc-transitively on \(\Gamma\). Today, more than half a century later, a lot is known about half-arc-transitive graphs and graphs admitting half-arc-transitive group actions, in particular on the tetravalent ones, but with every new result come new interesting questions and open problems.
In this talk I will highlight some recent and ongoing research on tetravalent graphs admitting half-arc-transitive group actions, propose a few possible directions for research on these graphs and present some questions and open problems which I find interesting.
Let \(R\) be a group and let \(S\) be a subset of \(R\). The Cayley digraph on \(R\) with connection set \(S\), denoted \(\mathrm{Cay}(R,S)\), is the digraph with vertex-set \(R\) and with \((g,h)\) being an arc if and only if \(hg^{-1}\in S\). It is an easy observation that \(R\) acts regularly as a group of automorphisms of \(\mathrm{Cay}(R,S)\) by right multiplication and hence \(R\le \mathrm{Aut}(\mathrm{Cay}(R,S))\).
Although the definition of a Cayley digraph forces the automorphism group of such a digraph to contain a group acting regularly, there is nothing in the definition that tells us whether or not such a digraph has any other automorphisms. When considering questions of structure and isomorphism, determining the full automorphism group of a digraph is a very important question. In the case of a Cayley digraph on a group $R$, a major first step in finding the answer to this question is to determine whether \(R\) is in fact the full automorphism group of this digraph. When it is, \(\mathrm{Cay}(R,S)\) is called a DRR (for digraphical regular representation).
Babai and Godsil made the following conjecture.
Let \(R\) be a group of order \(r\). The proportion of subsets \(S\) of \(R\) such that \(\mathrm{Cay}(R,S)\) is a \(\mathrm{DRR}\) goes to \(1\) as \(r\to\infty\).
In this talk, we discuss a recent solution of this conjecture, its natural extension of undirected graphs and some relation to natural questions in the theory of finite permutation groups.
A planar rod configuration is a configuration of points and lines in the Euclidean plane, not necessarily with the same number of points on each line, nor the same number of lines through each point. A motion of a rod configuration is a motion of the points and the lines preserving the distance between collinear points. The rod configuration is rigid if the only motions it admits are the Euclidean rigid motions. While it is trivial to find geometric realizations of graphs in the Euclidean plane, this is not in general the case for combinatorial configurations. In 1927, Geiringer proved that the infinitesimal rigidity of graphs realized in the Euclidean plane can be determined using combinatorial methods. Her theorem was rediscovered by Laman in 1970. In 1989, Whiteley generalized Geiringer’s result to certain graphs with their edges on the lines of a point and line configuration. He then used this result to show that certain sparse (“independent”) combinatorial configurations always can be realized in the Euclidean plane, and was able to determine the infinitesimal rigidity of such a realization using a combinatorial count. In 2008, Jackson and Jordán provided a combinatorial characterization of rigid planar rod configurations for the case when the dual configuration is a graph. Their result was the planar case of the long-standing Molecular conjecture, which was subsequently proved by Katoh and Tanigawa in 2011. In this talk I will give an overview of the combinatorial methods that are used to determine the rigidity of planar rod configurations and propose a way to solve the question in general.
This is joint work with Signe Lundqvist and Lars-Daniel Öhman.
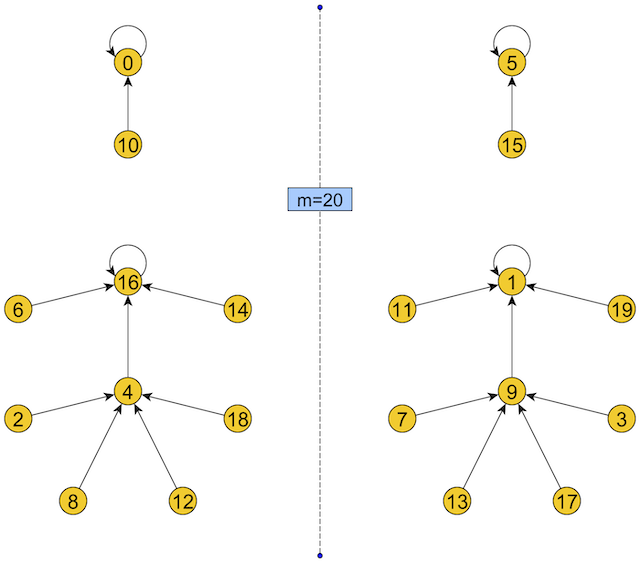
Let \(H_m=\{0,1,\dots,m-1\}\), where \(m\ge2\) is a fixed integer called modulus. Consider the function \(f(x)=x^2\pmod{m}\) acting on \(H_m\).
This function induces a digraph \(\cal G\) (it is called discrete iteration graph, the name comes from a more general approach) such that the vertices are the elements of \(H_m\), and arch connects \(x\) and \(f(x)\) for every \(x\in H_m\). The main interest is the structure of \(\cal G\), in particular the symmetry of that. We call a discrete iteration graph symmetric if its connected components can be partitioned into isomorphic pairs.
Suppose that the prime factorization of \(m\) is
\(m=p_1^{\alpha_1} p_2^{\alpha_2}\cdots p_s^{\alpha_s},\)
where \(\alpha_i>0\), and \(p_i>p_j\) if \(i>j\). The following theorem provides a sufficient condition for the symmetry of the corresponding graph.
Theorem If \(p_1=2\) and \(\alpha_1\in\{1,2\}\), then the iteration graph is symmetric.
Here we illustrate \(\cal G\) by choosing \(m=20\).
In the talk, a survey on the symmetry of certain discrete iteration graphs is given.
Toroidal orientably regular maps are presented from various viewpoints: geometric, topological, group theoretic, and combinatorial. The elementary number theory of the order of the automorphism group is studied in terms of chirality, including a new proof for representing primes as a sum of two squares. Four very different proofs are given for the non-existence of regular maps in the klein bottle.
Given a \(G\)-arc-transitive graph, the local action is the permutation group induced by a vertex-stabiliser \(G_v\) on the neighbourhood of \(v\). It plays an extremely important role in the study of these objects.
The situation for digraphs is a little more complicated. One can consider both the in- and out-local-action, that is, the permutation group induced by a vertex-stabiliser on the corresponding in- and out-neighbourhood, respectively. Perhaps surprisingly, these two permutation groups need not be isomorphic, they may not even have the same order. We say that two permutation groups are compatible if they arise in this way, that is, as the in- and out-local action of some finite \(G\)-arc-transitive digraph. We will discuss the problem of characterising compatible permutation groups.
Consider edge-transitivity in tricirculant tetravalent graphs. There are 9 possible ‘diagrams’, of which four are easiily seen to be infeasible, and one more so seen but with difficulty. Of the remaining four, one is nearly completely classified, and two others have two or more families of edge-transitive examples.
The remaining diagram is the Wooly Hat. Earlier work by Hiroki Koike, Leah Berman, Elias Mochan and myself led to two families of vertex-transitive examples and a conjecture that no edge-tranisitive ones exist. Recent (very recent!) work, led by Primož Sparl, might succeed in proving the conjecture and classifying the vertex-tranitive graphs of this family.
In this talk, I will discuss the characterisation of the primitive 2-closed groups \(G\) of rank at most four that are not the auttomorphism group off a graph or digraph, and we show that if the degree is at least 2402 then there are just two infinite families or \(G\leq {\rm A\Gamma L}_1(p^d)\), the 1-dimensional affine semilinear group. To the best of our knowledge, these are the first known examples of non-regular 2-closed groups that are not the automorphism group of a graph or digraph.
This is a joint work with Michael Giudici and Luke Morgan